矩阵分解
针对协同过滤算法的头部效应明显、泛化能力弱的问题,矩阵分解算法被提出。矩阵分解在协同过滤算法中“共现矩阵”的基础上,加入了隐向量的概念,加强了模型处理稀疏矩阵的能力。
推荐过程
不同于协同过滤,矩阵分解算法希望为每一个用户和商品生成一个隐向量,将用户和视频定位到隐向量表示的表示空间上,距离相近的用户和商品表示兴趣特点接近,在推荐的过程中就应该把距离相近的商品推荐给目标用户。
其中,用户和物品的隐向量是通过矩阵分解协同过滤生成的共现矩阵得到的,如下图所示。
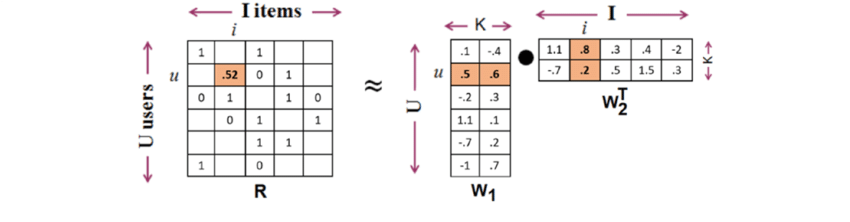
矩阵分解算法将m×n维的共线矩阵R分解为m×k维的用户矩阵W1和k×n的物品矩阵W2相乘,其中k为隐向量的维度。k的大小决定了隐向量表达能力的强弱。k越小,隐向量包含的信息越少,模型的泛化能力越高。此外,k的取值还与矩阵分解的求解复杂度直接相关。
最后,用户u对物品i的预估评分就是用户u对应的向量与物品i对应的向量的内积。
矩阵分解的求解过程
对矩阵进行分解的方式主要有三种:特征值分解、奇异值分解和梯度下降。其中特征值分解只能作用于方阵,显然不适用于分解用户-物品矩阵。
SVD分解
小小的复习一下SVD分解,手写一个简单的例子。(字好丑 /(ㄒoㄒ)/~~)

其实求到U1就可以了,后面的主要是完成一个完整的过程。
取对角阵中较大的k个元素作为隐含特征,删除对角阵的其他维度及U和V中对应的维度,至此就完成了隐向量维度为k的矩阵分解。
但是,SVD分解存在两点缺陷使其不宜作为互联网场景下矩阵分解的主要方法。
(1)奇异值分解要求原始的共现矩阵是稠密的。而互联网场景下大部分用户的历史行为非常少,导致矩阵稀疏。
(2)奇异值分解的计算复杂度达到了O(m×n2),这对于商品数量、用户数量几百万,上千万的互联网场景来说是不可接受的。
梯度下降
(1)矩阵分解的损失函数如下:
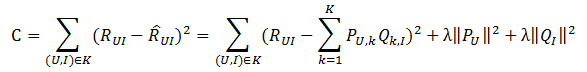
Pu,k表示用户的隐向量,Qk,i表示物品的隐向量。目标是要使C最小。后面两项是正则项,避免受个别“噪声点”的影响,模型的预测输出更加稳定。
(2)求其梯度:
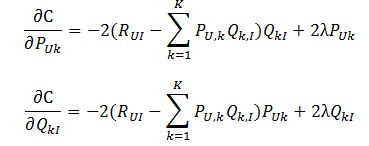
(3)然后梯度下降求其最小值:
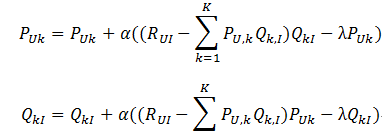
α为学习率。
(4)当迭代次数超过上限n或者损失低于阈值时,结束训练,否则循环第三步。
完成矩阵分解后,即可得到所有用户和物品的隐向量。对用户进行推荐时,可利用用户的隐向量与所有物品的隐向量进行逐一的内积运算,得到用户对所有物品的评分预测,再进行排序,得到最终的推荐列表。
隐向量的生成过程其实是对共现矩阵进行全局拟合的过程,因此隐向量其实是利用全局信息生成的,有更强的泛化能力。由于隐向量的存在,使任意的用户和物品之间都可以得到预测分值。
消除用户打分的偏差
由于用户的打分体系不同(例如有些人认为3分已经是很低的分数了,有人认为1分才是很差的评价),不同物品衡量标准也有所区别(电子产品和日用品的平均分差异有可能比较大)。为了消除这种偏差,常用的做法是在矩阵分解是加入用户和物品的偏差向量,如下图。
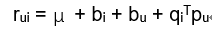
其中μ为全局偏差向量,bi是物品偏差系数(可使用物品i的所有评分的均值),bu是用户偏差系数(类似物品)。
与此同时,矩阵分解的目标函数也需要改变一点,损失函数及等号两边的偏差尽可能小,同时正则化项也要加上bi和bu。
矩阵分解的优点和局限性
优点
- 泛化能力强。一定程度上解决了数据稀疏问题。
- 空间复杂度低。无需存储庞大的用户相似性或物品相似性矩阵,只需存储用户和物品隐向量。空间复杂度由n2级别降低到(n+m)*k级别。
- 更好的扩展性和灵活性。矩阵分解的最终产物是用户和物品的隐向量,这与深度学习中的Embedding不谋而合,因此矩阵分解的结果也非常便于与其他特征进行组合和拼接,并便于与深度学习网络无缝结合。
局限性
与协同过滤一样,矩阵分解同样不便于加入用户、物品和上下文相关的特征,这使矩阵分解丧失了利用很多有效信息的机会
在缺乏用户历史行为时,无法进行有效的推荐。

