逻辑回归
主要优点:逻辑回归模型能够综合利用用户、物品、上下文等多种不同的特征,生成较为全面的推荐结果。
逻辑回归将推荐问题看成一个分类问题,通过预测正样本的概率对物品进行排序。
推荐过程
(1)将用户年龄、性别、物品属性、物品描述、当前时间、地点等特征转换成数值型特征向量(例如one-hot)。
(2)确定逻辑回归模型的优化目标,利用已有的数据样本对逻辑回归模型进行训练,确定逻辑回归模型内部的参数。
(3)在模型预测阶段,将特征向量输入逻辑回归模型,经过逻辑回归模型的计算,得到用户点击物品的概率。
(4)利用点击概率对所有候选物品进行排序,得到推荐列表。
数学形式
逻辑回归模型的推断过程可分为如下几步:
(1)将特征向量x = (x1,x2,…,xn)作为模型的输入。
(2)通过为各特征赋予相应的权重(w1,w2,….,wn),来表示各特征的重要性差异,将各特征进行加权求和(一般还会加一个偏置项b)。
(3)将加权求和的结果输入sigmoid函数,将其映射到0-1的区间,得到最终的点击率。
大致如下图。
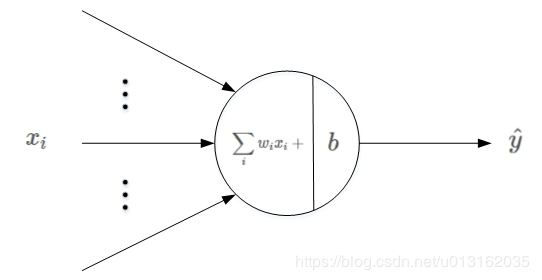
激活函数采用的是sigmoid函数。损失函数我们采用交叉熵损失,训练方法采用的是梯度下降。
sigmoid函数的求导过程:
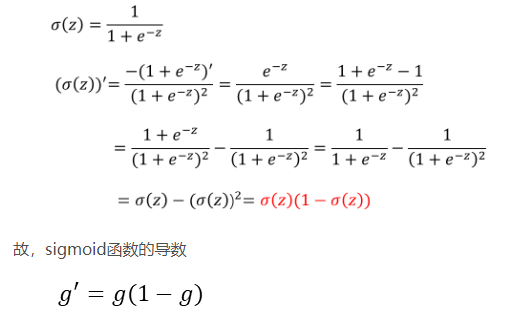
损失函数梯度求解过程:
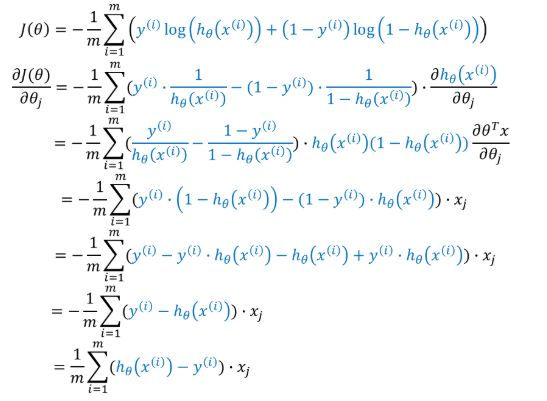
其中m为特征向量的维度,括号中的为交叉熵损失的一般形式,y(i)表示物品的标签(用户是否点击),hθ(x(i))表示模型输出的结果。
参数更新公式为:
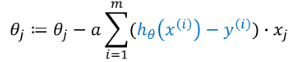
θj为上文中的权重wj。

逻辑回归模型的优势
数字含义上的支撑
逻辑回归作为广义线性模型的一种,它的假设是因变量y服从于伯努利分布。那么在点击率预估这个问题上,点击事件是否发生就是模型的因变量y,而用户是否点击广告是一个经典的掷偏心硬币问题。因此CTR模型的因变量显然是服从伯努利分布的。所以,采用逻辑回归进行点击率预测是有物理意义的。
相比之下,线性回归假设因变量y服从高斯分布,这显然不是点击这类二分类问题的数学假设。
可解释性强
逻辑回归使用各特征的加权和是为了综合不同特征对点击率的影响,从而不同特征的重要程度不一样,所以为不同特征指定不同的权重,在点击率模型的预测有偏差时可以定位到是哪些因素影响了最后的结果,最后通过sigmoid函数使其值能够映射到0-1区间,正好符合点击率的物理意义。
工程化的需要
逻辑回归模型易于并行化、模型简单、训练开销小使其在较大规模的数据面前有明显的优势。(一般公司不会贸然加大计算资源的投入)。
逻辑回归模型的局限性
表达能力不强,无法进行特征交叉、特征筛选等一系列操作。为了解决这一问题,推荐模型朝着复杂化的方向继续发展,如后面的因子分解机等模型。

