因子分解机
在推荐中仅利用单一特征而非交叉特征进行判断的情况下,有时不仅是信息损失的问题,甚至会得出会得出错误的结论。
辛普森悖论
在对样本进行分组研究的时候,在分组比较中都占优势的一方,在总评中有时反而是劣势的一方,这种有悖常理的现场被称为“辛普森悖论”。
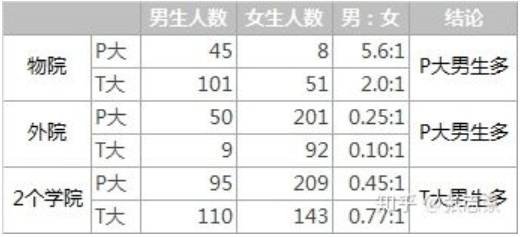
由图可看出无论是物院还是外院都是P大男生比例大,但合计是T大男生比例大,这就是所谓的辛普森悖论。
在上述的例子中,分组实验相当于使用“院系”+“学校”的组合特征来判断哪个学校男生多,而汇总实验则用“学校”这一个特征判断哪个学校男生多。汇总实验对高维特征进行了合并,损失了大量的有效信息,因此无法正确的刻画数据模式。
逻辑回归只对单一特征做简单加权,不具备进行特征交叉生成高维组合特征的能力,因此表达能力很弱,甚至可能得出像“辛普森悖论”那样的错误结论。因此,通过改造逻辑回归模型,使其具备特征交叉的能力是必要的。
FM模型
为了解决逻辑回归不具备特征交叉的能力,2010年,Rendle提出了FM模型。
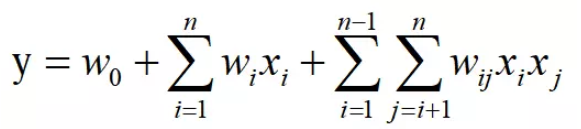
上图为FM模型的数学形式,与逻辑回归相比在后面加上了一个特征交叉项。FM为每个特征学习了一个隐权重向量,在特征交叉时,使用两个特征隐向量的内积作为交叉特征的权重,即上式中的Wij。
本质上,FM引入隐向量的做法,与矩阵分解用隐向量代表用户和物品的做法异曲同工。可以说,FM是将矩阵分解隐向量的思想进一步扩展,从单纯的用户、物品隐向量扩展到所有特征上。
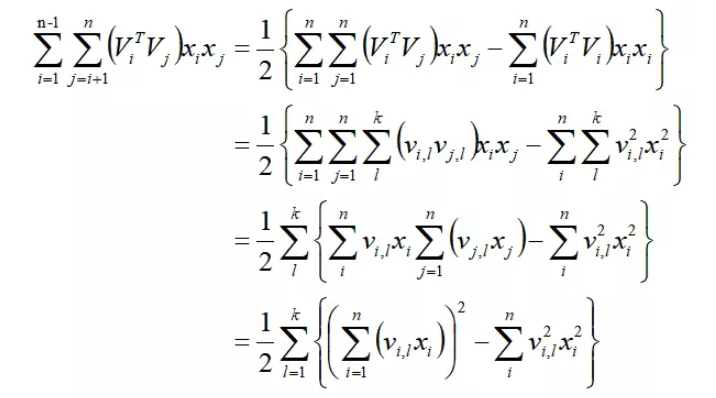
其中ViT Vj代表的就是上面的Wij,即交叉项的权重。通过上述计算,可将FM的训练复杂度从O(n2)降低到O(nk)。
FM模型的优点
隐向量的引入使FM能更好地解决数据稀疏性的问题。举例来说,在某商品的推荐下,样本有两个特征,分别是频道和品牌,某训练样本的特征组合是(ESPN,Adidas)。在FM中,ESPN的隐向量也可以通过(ESPN,Gucci)样本进行更新,Adidas的隐向量也可以通过(NBC,Adidas)样本进行更新,这大幅度降低了模型对数据稀疏性的要求。甚至对于一个从未出现过的特征组合(NBC,Gucci)样本进行更新,由于模型之前已经分别学习过NBC和Gucci的隐向量,具备了计算该特征组合权重的能力。
在工程方面,FM同样可以使用梯度下降法进行学习,使其不失灵活性和实时性。相比之后深度学习模型复杂的网络结构导致难以部署和线上服务,FM较容易实现的模型结构使其线上推断的过程相对简单,也更容易进行线上部署和服务。因此,FM在2012-2014年前后,成为业界主流的推荐模型之一。

